TD3 - Écoulements laminaire permanents de fluides classiques incompressibles.
Exercice 1
On considère l'écoulement unidirectionnel laminaire permanent d'un fluide classique incompressible non pesant entre deux plans horizontaux parallèles espacés d'une hauteur \(h=2y_0\).
La paroi inférieure est immobile alors que la paroi supérieure est en mouvement à la vitesse uniforme \(\overrightarrow{w_0}\)
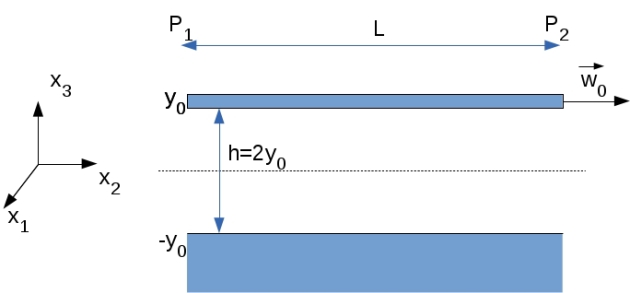
\(\overrightarrow{w_0}=\left( \begin{array}{lcr} w_1&=&0 \\ w_2&=w_0=&cte \\ w_3&=&0 \end{array} \right)\) est le vecteur vitesse de la plaque supérieure et \(\vec{V}=\left( \begin{array}{c} V_1=0 \\ V_2(x_2,x_3) \\ V_3=0 \end{array} \right)\) le vecteur vitesse du fluide.
Question
Déterminer le profil des vitesses (l'expression des équations de Navier-Stokes en coordonnées cartésiennes est donnée en annexe A).
Indice
Équation de continuité : \(div \vec V = 0 \Rightarrow \frac{\partial V_2}{\partial x_2}=0 \Rightarrow V_2(x_3)\)
Indice
Équation de Navier-Stokes : \(\rho \frac{d \vec V}{dt}=-\overrightarrow{grad} P+\underbrace{\rho \vec g}_{\text{\normalsize{négligeable}}} +\mu \Delta \vec V=-\nabla P + \mu \Delta \vec V\)
Indice
\(\left\{\begin{array}{l}\left.\begin{array}{l} \frac{\partial P}{\partial x_1}=0\\ \frac{\partial P}{\partial x_3}=0\end{array} \right\}\rightarrow P(x_2)\\\frac{\partial P}{\partial x_2}=\mu \frac{\partial^2 V_2}{\partial x_3^2}=\mu\frac{d^2 V_2}{d x_3^3}\end{array}\right.\)
Indice
Par symétrie, \( \frac{\partial^2 V_2}{\partial x_1^2}=0\)
Indice
\(V_2\) ne dépend que de \(x_3\), \(P\) ne dépend que de \(x_2\) \(\Rightarrow \frac{d P}{d x_2}=\mu\frac{\partial^2 V_2}{\partial x_3^2}=cte\)
\(cte=\frac{\Delta P}{L}=\frac{P_2-P_1}{L}\) que l'on peut aussi retrouver en disant \(\left.\begin{array}{l}P^*=cte. x_2+A\\x_2=0\rightarrow P=P_1=A\\ x_2=L\rightarrow P=P_2=cte.L.A=cte.L.P_1\end{array}\right\}\Rightarrow cte=\frac{P_2-P_1}{L}\)
Indice
\(\frac{\partial ^2V_2}{\partial x_3^2}=\frac 1\mu\left( \frac{\partial P}{\partial x_2}\right)\)
\(\frac{\partial V_2}{\partial x_3}=\frac 1\mu x_3\left( \frac{d P}{d x_2}\right)+A\)
\(V_2(x_3)=\frac{1}{2\mu}\left( \frac{d P}{d x_2}\right)x_3^2+Ax_3+B\)
Indice
CL :
\(V_2(-y_0)=0=\frac{1}{2\mu}\left( \frac{d P}{d x_2}\right)y_0^2-Ay_0+B\) (1)
\(V_2(y_0)=w_0=\frac{1}{2\mu}\left( \frac{d P}{d x_2}\right)y_0^2+Ay_0+B\) (2)
(1)+(2)\(\Rightarrow 2B+\frac 1\mu\left(\frac{d P}{d x_2}\right)y_0^2=w_0\)
\(B=\frac 12 w_0-\frac{1}{2\mu}\left(\frac{\partial P}{\partial x_2}\right)y_0^2\)
\(A=\frac{1}{2\mu}\cancel{\left(\frac{\partial P}{\partial x_2}\right)}y_0+\frac 12 \frac{w_0}{y_0} -\frac{1}{2\mu}\cancel{\left(\frac{\partial P}{\partial x_2}\right)}y_0\)
\(A=\frac 12 \frac{w_0}{y_0}\)
Indice
\(V_2(x_3)=\frac{1}{2\mu}\left(\frac{d P}{d x_2}\right)x_3^2 + \frac{w_0}{2y_0}x_3+\frac{w_0}{2}-\frac{1}{2\mu}\left(\frac{d P}{d x_2}\right)y_0^2\)
\(V_2(x_3)=\frac{1}{2\mu}\left(\frac{d P}{d x_2}\right)\left(x_3^2-y_0^2\right) + \frac{w_0}{2}\left(1+\frac{x_3}{y_0}\right)\)
Solution
\(V_2(x_3)=\frac{1}{2\mu}\left(\frac{\Delta P}{L}\right)\left(x_3^2-y_0^2\right) + \frac{w_0}{2}\left(1+\frac{x_3}{y_0}\right)\)
répartition des vitesses parabolique mais non symétrique
Écoulement plan de Couette
Le gradient de pression est supposé nul.
Question
1) Donner le profil des vitesses dans ce cas particulier.
Indice
\(\overrightarrow{grad} P=0\Rightarrow \frac{dP}{dx_2}=0=\frac{\Delta P}{L}\) d'où \(\frac{\partial^2V_2}{\partial x_3^2}=0\)
\(\frac{\partial V_2}{\partial x_3}=A\) et \(V_2=Ax_3+B\)
\(x_3=-y_0\rightarrow V_2=0=-Ay_0+B\rightarrow B=\frac{w_0}{2}\)
\(x_3=y_0\rightarrow V_2=w_0=Ay_0+B\rightarrow A=\frac{w_0}{2y_0}\)
Solution
\(V_2(x_3)=\frac{w_0}{2}\left(1+\frac{x_3}{y_0 }\right)\)
Question
2) Exprimer la vitesse maximale
Solution
Distribution des vitesses linéaires \(V_{max}=w_0\)
Question
3) Exprimer le débit et la vitesse moyenne débitante de l'écoulement.
Indice
\(\displaystyle Q=\iint_S\vec V \vec n dS\)
Indice
\(\displaystyle Q=\int_{-y_0}^{y_0}V_2(x_3)ldx_3=\int_{-y_0}^{y_0}\frac{w_0l}{2}\left( 1+\frac{x_3}{y_0}\right) dx_3\)
\(Q=w_0ly_0+\frac{w_0l}{2}\left[\frac12 \frac{x_3^2}{y_0}\right]_{-y_0}^{y_0}=w_0ly_0\)
Solution
\(Q=\overline{V}S=\overline{V}l2y_0=w_0ly_0\)
\(\overline{V}=\frac{w_0}{2}\) vitesse moyenne débitante
Question
4) Déterminer la contrainte visqueuse exercée par la paroi en mouvement sur le fluide.
En déduire :
Le coefficient de friction \(C_f\) en fonction du nombre de Reynolds,
La force de frottement exercée par la paroi en mouvement sur le fluide.
Indice
Tenseur des contraintes visqueuses :
\(\tau=\left(\begin{array}{l c r} 0&0&0\\0&0&\tau_{23}\\0&\tau_{32}&0\end{array}\right)\)
Indice
\(\overrightarrow{\sigma_V}(y_0)=\tau(y_0)\vec n\) avec\(\vec n=\) normale sortante \(=\vec e_3=\left(\begin{array}{l}0\\0\\1 \end{array}\right)\) donc :
\(\overrightarrow{\sigma_V}(y_0)=\left(\begin{array}{lcr}0&0&0\\ 0&0&\tau_{23}(y_0)\\ 0&\tau_{32}(y_0)&0 \end{array}\right)\left(\begin{array}{l}0\\ 0\\ 1 \end{array}\right)=\left(\begin{array}{l}0\\ \tau_{23}(y_0)\vec e_2\\ 0 \end{array}\right)\) contrainte selon \(\vec e_2\) sur une facette perpendiculaire à \(\vec e_3\)
Indice
\(|| \overrightarrow{\sigma _V}(y_0) ||=\tau_P=|\tau_{23}(y_0)|=\left|\mu\left(\frac{\partial V_2}{\partial x_3}+\cancel{\frac{\partial V_3}{\partial x_2}}\right)\right|_{y_0}=\mu\frac{w_0}{2y_0}\)
Indice
\(\displaystyle C_f=\frac{\tau_P}{\left(\rho \frac{\overline{V}}{2}^2\right)}=\frac{\mu w_02}{\rho \overline{V}^2 2y_0}\)
Indice
On a \(Re=\frac{\rho V D_H}{\mu}\) avec \(D_H=4\frac{2y_0l}{2l}=4y_0\) (\(2l\) car il n'y a pas de parois latérales)
Solution
donc \(C_f=\frac{4}{Re}\frac{w_0}{\overline{V}}\) avec \(\overline{V}=\frac{w_0}{2}\Rightarrow C_f=\frac{8}{Re}\)
Solution
Force de frottement exercée par la paroi en mouvement sur le fluide :
\(\displaystyle \vec F=\iint_S \overrightarrow{\sigma_V}(y_0)dS=\int_0^l\int_0^L\mu\frac{w_0}{2y_0}\vec e_2 dx_1dx_2=\mu \frac{w_0}{2y_0}lL\vec e_2\)
Question
5) Calculer la valeur du coefficient d'énergie cinétique \(\alpha\) permettant d'exprimer la charge en fonction de la vitesse moyenne débitante.
Indice
\(H=P^*+\frac{V_2^2(x_3)}{2g}\)
\(\overline{H}=P^*+\alpha \frac{\overline{V}^2}{2g}\)
Indice
\(\displaystyle \alpha=\frac 1S\iint_S\left( \frac{V_2(x_3)}{\overline{V}}\right)^3dS\) avec \(V_2(x_3)=\frac{w_0}{2}\left(1+\frac{x_3}{y_0}\right)=\overline{V}\left(1+\frac{x_3}{y_0}\right)\)
Indice
donc
\(\displaystyle \alpha=\frac{1}{2y l}\int_0^l\int_{-y_0}^{y_0}\left(1+\frac{x_3}{y_0}\right)^3dx_1dx_3\)
\(\displaystyle =\frac{1}{2y l}\left[y_0\frac14\left(1+\frac{x_3}{y_0}\right)^4\right]_{-y_0}^{y_0}=\frac{16}{8}=2\)
Solution
donc \(\overline{H}=P^*+\frac{\overline{V}^2}{g}\)
Écoulement plan de poiseuille
Les deux parois sont immobiles.
Question
1)Donner le profil des vitesse dans ce nouveau cas particulier.
Indice
\(w_0=0\hspace{1cm}\overrightarrow{grad} P\neq 0\)
Indice
\(\Rightarrow \mu\frac{\partial^2V_2}{\partial x_3^2}=\frac{\partial P}{\partial x_2}=cte=\frac{\Delta P}{L}<0\) et \(\Delta P=P_2-P_1\)
Indice
\(V_2(x_3)=\frac{1}{2\mu}\left(\frac{\Delta P^*}{L}\right)x_3^2+Ax_3+B\)
\(x_3=-y_0\rightarrow V_2(-y_0)=0=\frac{1}{2\mu}\left( \frac{\Delta P}{L}\right)y_0^2-Ay_0+B\)
\(x_3=y_0\rightarrow V_2(y_0)=0=\frac{1}{2\mu}\left( \frac{\Delta P}{L}\right)y_0^2+Ay_0+B\)
\(\Rightarrow B=-\frac{1}{2\mu}\left(\frac{\Delta P}{L}\right)y_0^2\) et \(A=0\)
Solution
\(V_2(x_3)=\frac{1}{2\mu}\left( \frac{\Delta P}{L}\right) \left( x_3^2-y_0^2\right)=-\frac{1}{2\mu}\left(\frac{\Delta P}{L}\right) y_0^2\left(1-\frac{x_3^2}{y_0^2}\right)\)
Question
Question
3) Exprimer le débit et la vitesse moyenne débitante de l'écoulement.
Indice
\(\displaystyle Q=\int_{-y_0}^{y_0}V_2(x_3)dS=\int_{-y_0}^{y_0}V_2(x_3)ldx_3\)
\(\displaystyle =\frac{1}{2\mu}\left(\frac{\Delta P}{L}\right) l\left[\frac13x_3^2\right]_{-y_0}^{y_0}-\frac{1}{2\mu}\left(\frac{\Delta P}{L}\right) ly_0^2\left[x_3\right]_{-y_0}^{y_0}\)
\(=\displaystyle \frac{\cancel{2}}{3}y_0^3\frac{1}{\cancel{2}\mu}\left(\frac{\Delta P}{L}\right) l-\frac{1}{\cancel{2}\mu}\left(\frac{\Delta P}{L}\right) l\cancel{2}y_0^3\)
Solution
\(Q=-\frac{2}{3}y_0^3\frac{1}{\mu}\left(\frac{\Delta P}{L}\right) l\)
Solution
Vitesse moyenne débitante :
\(Q=\overline{V}S\)
\(\overline{V}\cancel{l2y_0}=-\frac{\cancel{2}}{3}y_0^{\cancel{3}2}\frac{1}{\mu}\left(\frac{\Delta P}{L}\right)\cancel{l}\)
\(\overline{V}=-\frac{1}{3}\frac{y_0^2}{\mu}\left(\frac{\Delta P}{L}\right)=\frac23 V_{max}\)
Complément :
\(V_2(x_3)=V_{max}\left(1-\frac{x_3^2}{y_0^2}\right)=\frac 32\overline{V}\left(1-\frac{x_3^2}{y_0^2}\right)\)
Question
4) Déterminer la contrainte visqueuse exercée par la paroi en mouvement sur le fluide.
En déduire :
Le coefficient de friction \(C_f\) en fonction du nombre de Reynolds,
La force de frottement exercée par la paroi en mouvement sur le fluide.
Indice
Comme précédemment,
\(\tau_P=||\overrightarrow{\sigma_V}(y_0)||=|\tau_{23}(y_0)|\) et \(\overrightarrow{\sigma_V}=\tau_{23}(y_0)\vec e_2\)
Indice
\(\displaystyle \Rightarrow \tau_{23}(y_0)=\mu\left(\frac{\partial V_2}{\partial x_3}\right)_{x_3=y_0}=\mu\frac 1\mu \left(\frac{\Delta P}{L}\right) y_0=\left(\frac{\Delta P}{L}\right)y_0<0\)
Indice
\(\displaystyle \Rightarrow \tau_P=|\tau_{23}(y_0)|=-\tau_{23}(y_0)\)
Indice
\(C_f=\frac{\tau_P}{\left(\rho\frac{\overline{V}^2}{2}\right)}=-\frac{\left(\frac{\Delta P}{L}\right)y_0}{\left(\rho\frac{\overline{V}^2}{2}\right)}=-\frac{\cancel{\left(\frac{\Delta P}{L}\right)y_0}\ 2}{\rho\overline{V}\left(-\frac{1}{3}\cancel{\left(\frac{\Delta P}{L}\right)}\frac{y_0^{\cancel{2}}}{\mu}\right)}\)
Solution
\(C_f=6\frac{\mu}{\rho \overline{V}y_0}=\frac{24}{Re}\)
Solution
\(\displaystyle \vec F = \iint_S\overrightarrow{\sigma_V}(y_0)dS=\int_0^L\int_0^l\frac{P_2-P_1}{L}y_0 \vec e_2 dx_1dx_2\)
\(=\frac{P_2-P_1}{L}y_0 \vec e_2 l L=(P_2-P_1)ly_0\vec e_2 <0\)
Question
5) Exprimer le coefficient de pertes de charge linéaires \(f\), également en fonction du nombre de Reynolds.
Indice
Coefficient de pertes de charge
\(H_1=H_2+\Delta H_L\) avec \(\Delta H_L=\) pertes de charges linéaires \(=f\frac{\overline{V}^2}{2g}\frac{L}{D_H}\) avec \(D_H=4\frac SP=4\frac{2y_0l}{2l}=4y_0\)
Indice
\(H=\frac{P^*}{\rho g}+\frac{V^2}{2g}\approx \frac{P}{\rho g}+\frac{V^2}{2g}\)
Indice
\(\Delta H_L=H_1-H_2=\frac{P_1-P_2}{\rho g}=-\frac{\Delta P}{\rho g}=\frac{3\overline{V}\mu L}{y_0^2 \rho g}\)
Indice
\(\Delta H_L=\frac{3\overline{V}\mu \cancel{L}}{y_0^2 \rho \cancel{g}}=f\frac{\overline{V}^2}{2\cancel{g}}\frac{\cancel{L}}{4y_0}\)
Solution
\(f=\frac{24 \mu}{\rho \overline{V}y_0}=\frac{96}{Re}\) avec \(Re=\frac{\rho\overline{V} D_H}{\mu}\)
Question
5) Calculer la valeur du coefficient d'énergie cinétique \(\alpha\).
Indice
\(\overline{H}=P^*\alpha \frac{\overline{V}^2}{2g}\) et \(H=P^* \frac{V^2}{2g}\)
Indice
\(\displaystyle{ \alpha = \frac 1S \iint_S \left( \frac{V_2(x_3)}{\overline{V}}\right)^3dS=\frac{1}{2ly_0}\int_0^l\int_{-y_0}^{y_0}\left( \frac 32\right)^3\left( 1-\frac{x_3^2}{y_0^2}\right)^3dx_1dx_3}\)
\(=\frac{l}{2ly_0}\frac{27}{8}\displaystyle \int_{-y_0}^{y_0}\left( 1-\frac{x_3^2}{y_0^2}\right)^3dx_3\)
Indice
rappel \((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
\(\displaystyle \alpha =\frac{27}{16y_0} \int_{-y_0}^{y_0}\left( 1-3\frac{x_3^2}{y_0^2} +3\frac{x_3^4}{y_0^4}-\frac{x_3^6}{y_0^6} \right)^3dx_3\)
\(=\frac{27}{16y_0} \left[\left( x_3-\frac{x_3^3}{y_0^2} +\frac 35\frac{x_3^5}{y_0^4}-\frac 17 \frac{x_3^7}{y_0^6} \right)^3\right]_{-y_0}^{y_0}\)
\(=\frac{27}{16y_0} \left(\cancel{y_0} -\cancel{y_0}+\frac 35 y_0-\frac 17 y_0+\cancel{y_0}-\cancel{y_0}+\frac 35 y_0-\frac 17 y_0\right)\)
Solution
\(\alpha = \frac{54}{35}\approx 1.54\)
Rhéomètre de Couette
On considère l’écoulement unidirectionnel laminaire permanent d'un fluide classique incompressible entre deux cylindre coaxiaux de hauteur \(h\). Le cylindre externe de rayon \(R_2\) est immobile alors que le cylindre interne de Rayon, \(R_1\) tourne à la vitesse angulaire \(\omega_1\)
l'écoulement est unidirectionnel c'est à dire que le vecteur vitesse du fluide est de la forme \(\vec V=V_\theta (r,\theta)\vec e\). De plus, par symétrie la pression motrice \(P^*\) ne dépend pas de la variable \(\theta\).
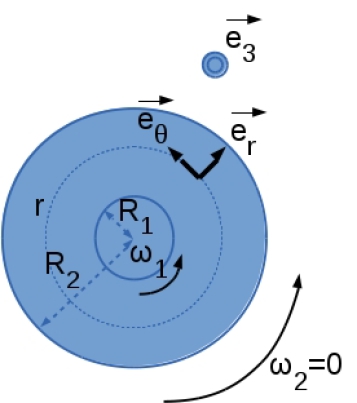
Question
1) Déterminer le profil des vitesse (l'expression des équations de Navier-Stokes en coordonnées cylindriques est donnée en annexe B)
Indice
Régime permanent, fluide incompressible
\(\vec V=V_\theta \vec e_\theta\) ou \(V_\theta\) de \(\vec V \left| \begin{array}{l} 0=V_r \\ V_\theta(r,\theta) \\ 0=V_3\end{array}\right.\)
\(\omega =\) vitesse angulaire \(=V_\theta r=Vr\)
Indice
\(\nabla \vec V = 0 = \frac 1r \frac{\partial}{\partial r}(rV_r)+\frac 1r \frac{\partial V_\theta}{d\theta}+\frac{\partial V_3}{\partial x_3}=0\)
\(\Rightarrow \frac{\partial V_\theta}{\partial \theta}=0\) donc \(V_\theta=f(r)\)
\(\vec V \left| \begin{array}{l} 0=V_r \\ V_\theta(r) \\ 0=V_3\end{array}\right.\)
Indice
Navier-Stokes
(1) \(-\rho \frac{V_\theta^2}{r}=-\frac{\partial P^*}{\partial r}\)
(2) \(0=-\frac 1r \require{cancel}\cancel{\underbrace{\frac{\partial P^*}{\partial \theta}}_{\text{par symétrie}}}+\mu \left[\frac 1r \frac{\partial}{\partial r}\left(r\frac{dV_\theta}{dr} \right)-\frac{V_\theta}{r^2}\right]\)
\(\frac 1r \frac{d}{d r}\left(r\frac{dV_\theta}{dr} \right)=\frac{V_\theta}{r^2}\)
\(\frac{d^2V_\theta}{dr^2}+\frac 1r\frac{dV_\theta}{d r}-\frac{V_\theta}{r^2}=0\)
\(\frac{d^2V_\theta}{dr^2}+\frac{d\frac{V_\theta}{r}}{dr}=0\)
(3) \(0=-\frac{\partial P^*}{\partial x_3}\)
Indice
Condition aux limites :
en \(r=R_1\), \(V_\theta =R_1\omega_1\)
en \(r=R_2\), \(V_\theta=R_2\omega_2=0\)
Indice
Résolution de l'équation différentielle linéaire du second ordre à coefficients non constants
\(\frac{d^2V_\theta}{dr^2}+\frac{d\frac{V_\theta}{r}}{dr}=0\)
\(\frac{d^2V_\theta}{dr^2}+\frac 1r\frac{dV_\theta}{d r}-\frac{V_\theta}{r^2}=0\)
Solution évidente, \(V_\theta=r\)
Indice
Variation de la constante :
\(V_\theta=k(r)r\)
\(V_\theta'=k'r+k\)
\(V_\theta''=k''r+2k'\)
Indice
\(\frac{d^2 V_\theta}{dr^2}+\frac 1r \frac{dV_\theta}{dr}-\frac{V_\theta}{r^2}=k''r+2k'+k'+\cancel{\frac kr}-\cancel{\frac kr}=0\)
\(k''r+3k'=0\)
Indice
\(\frac{k''}{k'}=-\frac 3r \rightarrow lnk'=-3lnr+C\)
\(k'=c_1\frac{1}{r^3}\)
\(k=-\frac 12 \frac{c_1}{r^2}+c_2\)
Indice
\(V_\theta (r)=-\frac 12\frac{c_1}{r}+c_2r=\frac{k_1}{r}+k_2r\)
Indice
Conditions aux limites :
\(\left\{ \begin{array}{l}R_1\omega_1=\frac{k_1}{R_1}+k_2R_1\\ \underbrace{R_2\omega_2}_{=0}=\frac{k_1}{R_2}+k_2R_2\end{array}\right.\)
\(\left\{ \begin{array}{l}k_1=\frac{R_2^2R_1^2(\omega_2-\omega_1)}{R_1^2-R_2^2}\rightarrow k_1=\frac{-R_2^2R_1^2\omega_1}{R1^2-R2^2} \\ k_2=\frac{R_1^2\omega_1-R_2^2\omega_2}{R_1^2-R_2^2}\rightarrow k_2=\frac{R_1^2\omega_1}{R_1^2-R_2^2} \end{array}\right.\)
Solution
\(V_\theta(r)=\frac{-R_2^2R_1^2\omega_1}{\left(R_1^2-R_2^2\right)r}+\frac{R_1^2\omega_1}{R_1^2-R_2^2} r\)
Question
2) Exprimer la contrainte visqueuse exercée par le cylindre en rotation sur le fluide.
Indice
Le rhéomètre calcule la viscosité à partir du mouvement du couple appliqué au cylindre tournant.
Soit h la hauteur du cylindre
avec \(dS=R_1d\theta dx_3\)
\(\overrightarrow{\sigma}=\) contrainte visqueuse exercée par la paroi du cylindre en rotation sur le fluide.
Indice
\(\overrightarrow{\sigma}(R_1)=\tau(R_1)\vec u\) avec \(\vec u =\) nommale sortante du fluide \(=(-\vec e_r)\) et \(\tau(R_1)=\) tenseur des contraintes visqueuses à la paroi du cylindre mobile.
Indice
\(\tau(R_1)=\left(\begin{array}{l c r}\tau_{rr}(R_1) & \tau_{r\theta}(R_1)&\tau_{r3}(R_1) \\ \tau_{\theta r}(R_1) & \tau_{\theta\theta}(R_1) & \tau_{\theta 3}(R_1) \\ \tau_{3r}(R_1)& \tau_{3\theta}(R_1) & \tau_{33}(R_1)\end{array}\right)=\left(\begin{array}{l c r}0 & \tau_{r\theta}(R_1)&0 \\ \tau_{\theta r}(R_1) & 0 & 0 \\ 0&0&0\end{array}\right)\)
Indice
\(\tau(R_1)(\vec e_r)=\left(\begin{array}{l c r}0 & \tau_{r\theta}(R_1)&0 \\ \tau_{\theta r}(R_1) & 0 & 0 \\ 0&0&0\end{array}\right)\left(\begin{array}{c}-1\\0\\0\end{array}\right)=\left(\begin{array}{c}0\\-\tau_{\theta r}(R_1)\\0\end{array}\right)=-\tau_{\theta r}(R_1)\vec e_\theta\)
Indice
\(\tau_{\theta r}=\mu \left(\frac{\partial V_\theta}{\partial r}-\frac{V_\theta}{r}+\cancel{\frac 1r \frac{\partial V_r}{\partial \theta}}\right)=\frac{\mu R_1^2\omega_1}{R_2^2-R_1^2}\left(\cancel{-1}-\frac{R_2^2}{r^2}\cancel{+1}-\frac{R_2^2}{r^2}\right)\)
\(\Rightarrow \tau_{\theta r}(R_1)=-\frac{2\mu\omega_1R_2^2}{R_2^2-R_1^2}\)
Solution
donc \(\overrightarrow{\sigma}(R_1)=\frac{2\mu\omega_1R_2^2}{R_2^2-R_1^2} \vec e_\theta\)
Question
3) Déterminer le couple que doit fournir le moteur du rhéomètre pour mettre le cylindre interne en rotation à la vitesse angulaire \(\omega_1\). En déduire l'expression qui permet de calculer la viscosité du fluide.
Indice
\(\displaystyle \vec C = \iint_S \overrightarrow{OM}\land \overrightarrow{\sigma}(R_1)dS\) avec \(\overrightarrow{OM}=R_1\vec e_r\)
Indice
\(\left(\begin{array}{c}1\\0\\0\end{array}\right)\land \left(\begin{array}{c}0\\1\\0\end{array}\right)=\left(\begin{array}{c}0\\0\\1\end{array}\right)\)
\(\displaystyle \iint_S ||\overrightarrow{OM}\land\overrightarrow{\sigma}||\ [\vec e_r\land \vec e_\theta]\ dS=\iint_S ||\overrightarrow{OM}|| \ ||\overrightarrow{\sigma}|| sin\left(\overrightarrow{OM},\overrightarrow{dF}\right) \vec e_3dS\)
\(\displaystyle =\vec e_3 \iint_S R_1\frac{2\mu \omega_1R_2^2}{R_2^2-R_1^2}R_1d\theta dx_3=\frac{2\mu \omega_1R_2^2 R_1^2}{R_2^2-R_1^2}\int_0^{2\pi} \int_0^h d_\theta dx_3 \vec e_3\)
Solution
\(||\vec C ||=\frac{2\mu \omega_1R_1^2 R_2^2 2\pi h}{R_2^2-R_1^2}\)
Solution
Donc pour le rhéomètre, pour un fluide newtonien, la formule de la viscosité est :
\(\mu=\frac{||\vec C ||\left(R_2^2-R_1^2\right)}{4 \omega_1R_1^2 R_2^2 \pi h}\)
Remarque :
Par symétrie \(\displaystyle \vec F=\iint_S-\overrightarrow \sigma dS=\vec 0\) résultante des forces de frottement exercée par le fluide sur le cylindre en rotation.
\(\displaystyle \vec F=\iint_S-\overrightarrow \sigma (R_1) dS=\iint_S-\overrightarrow{\tau_{\theta r}}(R_1) \vec e_\theta dS=-\tau_{theta r}(R_1)\int_0^h\int_0^{2\pi} \vec e_\theta R_1 d\theta dx_3 \)
\(\displaystyle \vec F=-\tau_{\theta r}(R_1) R_1 h \int_0^{2\pi} \vec e_\theta =\vec 0\)