TD4 : Pertes de charge
Exercice 1
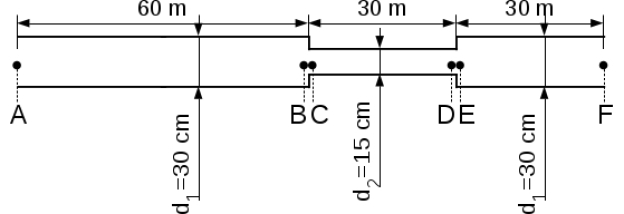
On considère un écoulement permanent d'eau de masse volumique \(\rho = 1000\ kgm^{-3}\) et de viscosité dynamique \(\mu = 1.4\ 10^{-3}\ Pa s\) dans l'installation représentée ci-dessous. L'eau est un fluide classique incompressible. En un point \(A\) du tuyau horizontal de \(30\ cm\) de diamètre et de rugosité \(\varepsilon_1=3\ 10^{-4}\ m\), la hauteur piézométrique est de \(60\ m\). A une distance de \(60\ m\)de \(A\), le diamètre du tuyau se rétrécit brusquement et passe à \(15 \ cm\) avec un rugosité \(\varepsilon_2 = 3\ 10^{-5}\ m\). A une distance de \(30\ m\) de là, le diamètre repasse brusquement à \(30 \ cm\). Le point \(F\) est situé à \(30\ m\) au delà de ce point.
Question
Pour une vitesse de \(2.41\ ms^{-1}\) dans les tuyaux de \(30\ cm\) de diamètre, calculer la charge et la hauteur piézométrique aux point \(A, B, C, D, E, F\).
Indice
En \(A\) :
\(\overline{H_A}=\frac{P_A}{\rho g}+\frac{\overline{V_1}^2}{2g}\)
Indice
Entre A et B :
\(\overline{H_A}=\overline{H_B}+\Delta H_{\displaystyle L_{AB}}\)
avec \(\Delta H_{\displaystyle L_{AB}}\) pertes de charges linéaires ou régulières.
\(\overline{H_B}=\overline{H_A}-\lambda_1\frac{\overline{V_1}^2}{2g}\frac{l_1}{d_1}\)
Indice
Indice
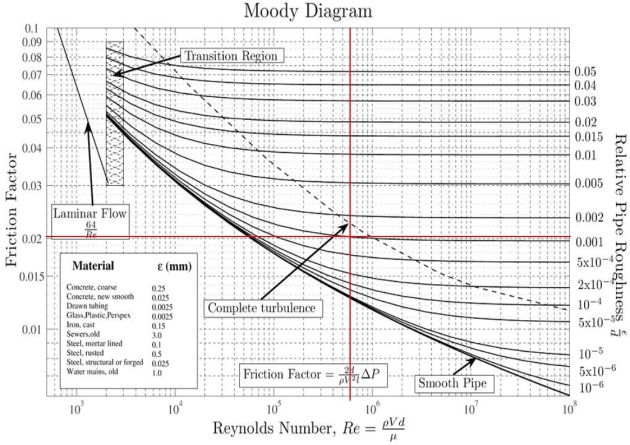
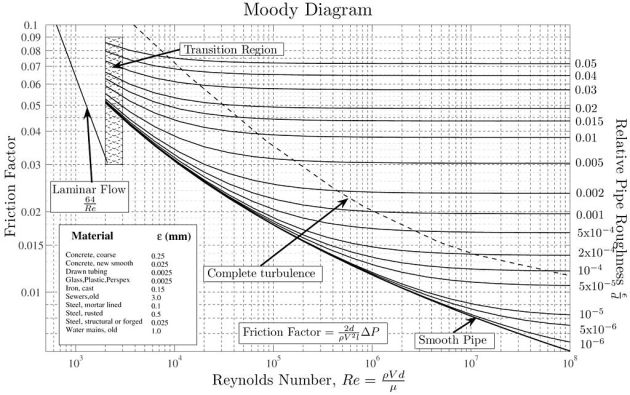
\(\frac{\varepsilon_1}{d_1} = 0.001\)
\(Re_1 = 5.16\ 10^5\)
\(\Rightarrow \lambda_1 = f_1\approx0.02\)
Indice
Entre B et C :
\(\overline{H_B}=\overline{H_C}+\Delta H_{\displaystyle L_{BC}}\)
avec \(\Delta H_{\displaystyle L_{BC}}\) pertes de charges singulières.
\(\overline{H_C}=\overline{H_B}-K_C \frac{\overline{V_{2}} ^2}{2g}\)
Indice
\(\overline{V_1} = 2.41\ ms^{-1} \Rightarrow \overline{V_2}=\frac{\overline{V_1}S}{s}=\overline{V_1}\left(\frac{d_1}{d_2}\right)^2=9.64\ ms^{-1}\)
Indice
Convergent brusque
\(\frac{d_1}{d_2} = 2 \Rightarrow k_c = 0.37\)
Indice
Entre C et D :
\(\overline{H_C}=\overline{H_D}+\Delta H_{\displaystyle L_{CD}}\)
\(\overline{H_D}=\overline{H_C}-\lambda_2\frac{\overline{V_2}^2}{2g}\frac{l_2}{d_2}\)
Indice
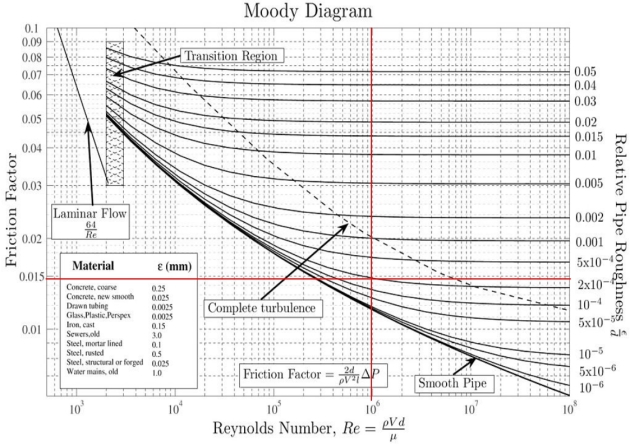
\(\frac{\varepsilon_2}{d_2} = 0.0002\)
\(Re_2 = 1.03\ 10^6\)
\(\lambda_2 \approx 0.015\)
Indice
Entre D et E :
\(\overline{H_D}=\overline{H_E}+\Delta H_{\displaystyle L_{DE}}\)
\(\overline{H_E}=\overline{H_D}-\frac{\left(\overline{V_2} -\overline{V_1}\right)^2}{2g}\)
Indice
Entre E et F :
\(\overline{H_E}=\overline{H_F}+\Delta H_{\displaystyle L_{EF}}\)
\(\overline{H_F}=\overline{H_E}-\lambda_1\frac{\overline{V_1}^2}{2g}\frac{l_3}{d_1}\)
Solution
points | de | Pertes de charge (m) | Cotes de la ligne de charge (m) = | \(\frac{V^2}{2g}\) (m) + | cotes de ligne piétzométrique (m) |
A | 60.29 | 0.3 | 60 | ||
B | A à B | 1.2 | 59.09 | 0.3 | 58.79 |
C | B à C | 1.75 | 57.34 | 4.74 | 52.6 |
D | C à D | 14.22 | 43.12 | 4.74 | 38.38 |
E | D à E | 2.66 | 40.46 | 0.3 | 40.16 |
F | E à F | 0.6 | 39.86 | 0.3 | 39.56 |
Exercice 2
D'un bassin de décantation, on veut évacuer un débit de \(8\ m^3s^{-1}\) d'eau par une conduite cylindrique horizontale de longueur \(L = 200 \ m\). On dispose pour cela d'une dénivellation de \(15 \ m\) et d'éléments de tuyau circulaire en ciment, de diamètre \(D=1\ m\). On suppose que la conduite est reliée au bassin amont par un raccord convenablement arrondi pour éviter toute perte de charge à l'entrée.
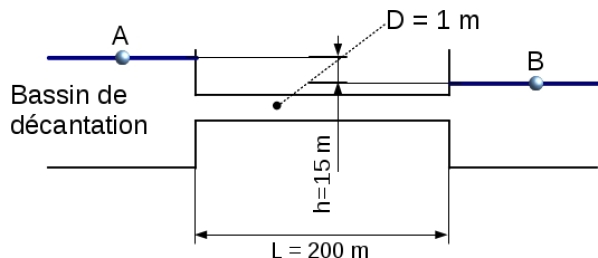
Question
L'évacuation est elle possible si on tient compte à la fois de la perte par frottement dans la conduite et de la perte de charge singulière correspondant à la sortie de la conduite ?
Pour un nombre de Reynolds supérieur à \(10^6\), on admettre que le coefficient de perte de charge garde la valeur constante : \(f=1.84\ 10^{-2}\).
La viscosité cinématique de l'eau vaut \(\nu = 1.14\ 10^{-6}\ m^2s^{-1}\) et l'accélération de la pesanteur vaut \(g=10\ ms^{-2}\).
Indice
\(\overline{H_A}=\overline{H_B}+\Delta H\)
\(\require{cancel}\cancel{\frac{P_{atm}}{\rho g}} + x_3^A + \cancel{\frac{V_A^2}{2g}} = \cancel{\frac{P_{atm}}{\rho g}} + x_3^B + \cancel{\frac{V_B^2}{2g}}+K\frac{\overline{V}^2}{2g}+f\frac{\overline{V}^2}{2g}\frac lD\)
Indice
\(\overline{V}=\frac qS = \frac{4q}{\pi D^2} = 10.18\ ms^{-1}\)
\(Re = \frac{\overline{V}D}{\nu} = 8.93\ 10^6\Rightarrow \lambda = 1.84\ 10^{-2}\)
\(\frac{\overline{V}^2}{2g}=5.18\ m\)
Solution
\(\Delta H = 24.24\ m\)
\(h = x_3^A-x_3^B=24.24\ m\) pour avoir un débit de \(8\ m^3s^{-1}\)
On ne dispose que d'un dénivelé de \(15\ m \Rightarrow\) impossible
Question
Étudier les solutions qui consisteraient :
a) à raccourcir la conduite
Indice
Pour que \(h=15\ m\) soit suffisant, \(l_1\) doit être tel que :
\(\frac{\overline{V}^2}{2g}+f\frac{\overline{V}^2}{2g}\frac{l_1}{D} = h\)
Indice
\(f\frac{l_1}{D}\frac{\overline{V}^2}{2g}=h-\frac Df\)
\(l_1 = \frac Df \frac{2g}{\overline{V}^2}h-\frac Df\)
Solution
\(l_1 = 103\ m\)
Question
b) à doubler la conduite sur une certaine longueur en utilisant un branchement et des canalisations de même diamètre.
Deux cas sont possibles suivant le sens d'écoulement de l'eau dans le branchement ; Quel est celui qui entraîne la moindre dépense en éléments de tuyaux ? On effectuera les calculs en négligeant la perte de charge singulière qu'introduit ce branchement.
Indice
On a \(q_v=8\ m^3s^{-1}=\overline V \frac{\pi D^2}{4}\)
\(D=D_1=D_2=1\ m\)
Indice
Cas 1 :
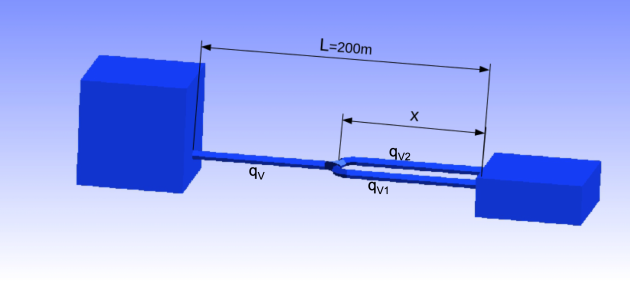
Indice
Cas 2 :
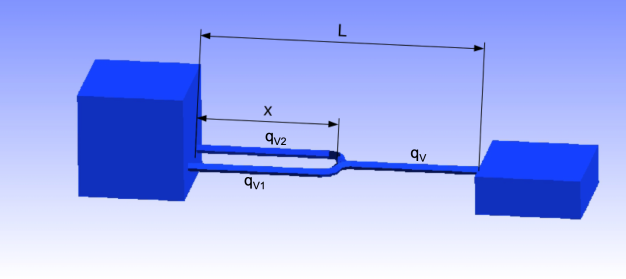
Indice
Sur la longueur x, à déterminer, on a un branchement en parallèle.
Indice
On doit résoudre le système :
\(\left\{\begin{array}{l} q_V = q_{V1}+q_{V2} \\ \Delta H_1=\Delta H_2 \end{array}\right.\)
Indice
\(\left\{\begin{array}{l r} \overline V \frac{\pi D^2}{4}=\overline V_1 \frac{\pi D_1^2}{4}+\overline V_2 \frac{\pi D_2^2}{4} & \\ \left(f_1\frac{L_1}{D_1}+1\right)\frac{\overline V_1^2}{2g}=\left(f_2\frac{L_2}{D_2}+1\right)\frac{\overline V_2^2}{2g} &\text{ pour le cas 1}\\ f_1\frac{L_1}{D_1}\frac{\overline V_1^2}{2g}=f_2\frac{L_2}{D_2}\frac{\overline V_2^2}{2g} &\text{ pour le cas 2} \end{array}\right.\)
avec \(D_1=D_2=D\) et \(L_1=L_2=x\)
Indice
Hypothèse à priori : on suppose que \(Re_1\) et \(Re_2>10^6\) donc \(f_1=f_2=1,84.10^{-2}\)
à vérifier après avoir calculé \(\overline V_1\) et \(\overline V_2\)
Indice
on a donc pour les cas 1 et 2 :
\(\left\{\begin{array}{l} \overline V = \overline V1 + \overline V2 \\ \overline V_1=\overline V_2 \end{array}\right.\)
d'où :
\(\overline V_1= \overline V_2 = \frac{\overline V}{2}=5,09\ ms^{-1}\)
Indice
On vérifie l'hypothèse :
\(\left\{\begin{array}{l} Re_1=\frac{\overline V_1 D_1}{\nu} =\frac{\overline V D}{2\nu}=\frac{Re}{2}=4,465.10^6 \\ Re_2=\frac{\overline V_2 D_2}{\nu} =\frac{\overline V D}{2\nu}=\frac{Re}{2}=4,465.10^6\end{array}\right.\)
Indice
Détermination de x
Indice
Cas 1 :
\(\Delta H_{A\rightarrow B} = f\frac{L-x}{D}\frac{\overline{V}^2}{2g}+\overbrace{f_1 \frac{L_1}{D_1}\left(\frac{\overline{V_1}}{2g}\right)^2+\frac{\overline V^2_1}{2g}}^{\Delta H_1}=h\)
\(\Delta H_{A\rightarrow B} = f\frac{L-x}{D}\frac{\overline{V}^2}{2g}+\underbrace{f_2\frac{L_2}{D_2}\left(\frac{\overline{V_2}}{2g}\right)^2+\frac{\overline V^2_2}{2g}}_{\Delta H_2}=h\)
\(\Delta H_{A\rightarrow B} = f\frac{L-x}{D}\frac{\overline{V}^2}{2g}+f\frac{x}{D}\frac{\overline{V}^2}{8g}+\frac{\overline{V}^2}{8g}=h\)
Indice
\(f\frac LD \frac{\overline V ^2}{2g}-f\frac xD \frac{\overline V ^2}{2g}+f\frac xD \frac{\overline V ^2}{8g} + \frac{\overline V ^2}{2g}=h\)
\(f\frac xD\left(\frac{\overline V ^2}{8g}-\frac{\overline V ^2}{2g} \right)=h-f\frac LD\frac{\overline V ^2}{2g}-\frac{\overline V ^2}{8g}\)
\(f\frac xD\left(-\frac{3\overline V ^2}{8g} \right)=h-f\frac LD\frac{\overline V ^2}{2g}-\frac{\overline V ^2}{8g}\)
Indice
\(x=\left(-\frac{8gD}{3\overline V^2 f} \right)\left(h-f\frac LD \frac{\overline V^2 }{2g} -\frac{\overline V^2 }{8g}\right)\)
Solution
\(x = \frac 43 L+\frac 13 \frac Df-\frac{8ghD}{3\overline{V}^2f}\)
\(x = 75\ m\)
d'où une longueur totale des éléments de tuyaux :
\(L = (L-L_2)+2L_2 = L+L_2 = 275\ m\)
Question
cas 2 :
Indice
\(\Delta H_{A\rightarrow B} = \overbrace{f_1 \frac{L_1}{D_1}\left(\frac{\overline{V_1}}{2g}\right)^2}^{\Delta H_1}+f\frac{L-x}{D}\frac{\overline{V}^2}{2g}+\frac{\overline V^2}{2g}=h\)
\(\Delta H_{A\rightarrow B} =\underbrace{f_2\frac{L_2}{D_2}\left(\frac{\overline{V_2}}{2g}\right)^2}_{\Delta H_2}+ f\frac{L-x}{D}\frac{\overline{V}^2}{2g}+\frac{\overline V^2}{2g}=h\)
\(\Delta H_{A\rightarrow B} = f\frac{x}{D}\frac{\overline{V}^2}{8g}+f\frac{L-x}{D}\frac{\overline{V}^2}{2g}+\frac{\overline{V}^2}{2g}=h\)
Indice
\(f\frac xD\left(\frac{\overline V ^2}{8g}-\frac{\overline V ^2}{2g} \right)=h-f\frac LD\frac{\overline V ^2}{2g}-\frac{\overline V ^2}{2g}\)
\(f\frac xD\left(-\frac{3\overline V ^2}{8g} \right)=h-f\frac LD\frac{\overline V ^2}{2g}-\frac{\overline V ^2}{2g}\)
Indice
\(x=\left(-\frac{8gD}{3\overline V^2 f} \right)\left(h-f\frac LD \frac{\overline V^2 }{2g} -\frac{\overline V^2 }{2g}\right)\)
Solution
\(x = \frac 43 L+\frac 43 \frac Df-\frac{8ghD}{3\overline{V}^2f}\)
\(x = 129.4\ m\)
longueur totale de tuyaux \( = L+L_3 = 329.4\ m\)
Le cas 1 est le plus intéressant car il permet de diminuer la perte de charge linéaire et la perte de charge singulière de raccordement au réservoir en aval contrairement au cas 2 qui ne diminue que la perte de charge linéaire.
Remarque :
Les autres possibilités pour diminuer les pertes de charge :
Augmentation du diamètre D
Diminution de f (réduire les aspérité)
Exercice 3
Soit le circuit hydraulique suivant :
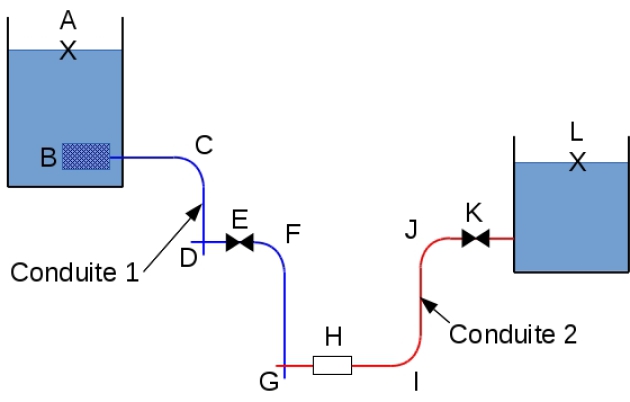
Conduite 1 : | Conduite 2 : |
\(L_1 = 45\ m\) | \(L_2 = 30\ m\) |
\(D_1 = 30\ cm\) | \(D_2 = 15\ cm\) |
\(f_1 = 0.025\) | \(f_2 = 0.02\) |
Coefficients K :
Filtre B : \(K_B = 8\)
Coudes C, F : \(K_C = K_F = 0.5\)
Té D : \(K_D = 0.7\)
Vanne E : \(K_E = 1\)
Croix G\( (30\ cm \times 15\ cm) : K_G = 0.7 \Rightarrow \Delta H _{S,G} = 0.7\frac{\overline{V}^2}{2g}\)
Appareil de mesure H : \(K_H = 6\)
Coudes I, J, : \(K_I=K_J = 0.5\)
Vanne K : \(K_K=3\)
Question
Quelle longueur équivalente de tuyau du type "conduite 2" peut remplacer le système de tuyau représenté ci dessus?
Indice
\(\overline{H_A} = \overline{H_L}+\Delta H_{A\rightarrow L}=h\)
Indice
\(\Delta H = \left( f_1\frac{L_1}{D_1}+K_B+K_C+K_D+K_E+K_F\right)\frac{V_{30}^2}{2g}+\left(f_2\frac{L_2}{D_2}+K_G+K_H+K_I+K_J+K_K+K_E\right)\frac{V_{15}^2}{2g}\)
Indice
De plus \(q=cte=V_{15}S_{15}=V_{30}S_{30}\)
\(V_{15}\frac{\pi D_2^2}{4}=V_{30}\frac{\pi D_1^2}{4}\)
\(V_{30}=V_{15}\left(\frac{D_2}{D_1}\right)^2=\frac{V_{15}}{4}\)
Indice
\(\Delta H = \frac{14.45}{16}\frac{V_{15}^2}{2g}+15.7\frac{V_{15}^2}{2g}\)
\(\Delta H = 16.6\frac{V_{15}^2}{2g}\)
Solution
Longueur de tuyau équivalente \(L\) telle que :
\(\Delta H = f_2\frac{L}{D_2}\cancel{\frac{V_{15}^2}{2g}}=\Delta H = 16.6\cancel{\frac{V_{15}^2}{2g}}\)
\(L=124.5\ m\)
Exercice 4 :
On transvase du lait d'un camion citerne dans un réservoir de stockage avec un débit constant de \(340\ L\ min^{-1}\). La conduite de longueur totale \(L=25\ m\) et de diamètre \(D=60\ mm\) comporte quatre coudes arrondis d'angle \(\theta=90°\) et de rayon de courbure \(R_C=120\ mm\) ainsi qu'une vanne à boisseau grande ouverte (\(K_V=0\)). Elle est connectée au ras de la paroi du camion citerne et débouche directement dans le réservoir à sa base. L'ensemble est en acier inoxydable de rugosité \(\varepsilon = 0.06\ mm\).
Données :
viscosité cinématique du lait entier : \(\nu = 1.93\ 10^{-6}\ m^2s^{-1}\),
masse volumique du lait entier : \(\rho = 1032\ kg\ m^{-3}\),
corrélation de Weisbach permettant de calculer le coefficient de perte de charge singulière pour les coudes :
\(K_c=\left[0.13+1.85\left(\frac{D}{2R_c}\right)^{7/2}\right]\left(\frac{\theta}{90}\right)\) (\(\theta\) en degrés)
Question
Déterminer la perte de charge de cette installation.
Indice
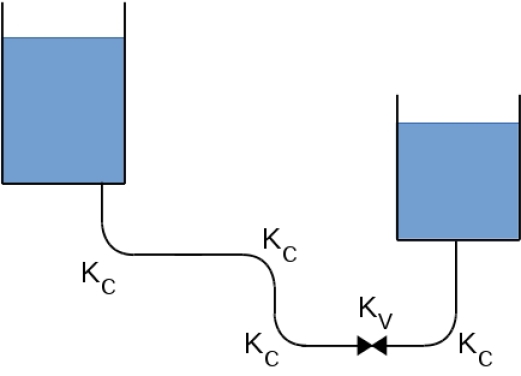
Indice
\(\Delta H=\Delta H_L+\Delta H_S = f\frac LD \frac {\overline{V}^2}{2g}+\underbrace{4K_c\frac{\overline{V}^2}{2g}}_{\displaystyle \text{4 coudes}}+\underbrace{\frac{\overline{V}^2}{2g}}_{\displaystyle \text{conduite à réservoir}}+\underbrace{K_V\frac{\overline{V}^2}{2g}}_{\displaystyle \text{0 car vanne ouverte}}+\underbrace{0.5\frac{\overline{V}^2}{2g}}_{\displaystyle \text{réservoir à conduite}}\)
\(\Delta H = \frac{\overline{V}^2}{2g}\left( f\frac LD+4K_c+1.5\right)\)
Indice
Calcul de \(\overline{V}\) :
\(q=340\ L\ min^{-1}=\frac{340\ 10^{-3}}{60}=5.67\ 10^{-3}\ m^3s{-1}\)
\(\overline{V}=\frac qS=\frac{4q}{\pi D^2}=2\ ms^{-1}\)
Indice
Calcule de f :
\(Re=\frac{\rho \overline{V} D}{\mu}=\frac{\overline{V}D}{\nu}=62176\approx 6.22\ 10^4\)
\(\frac\varepsilon D=0.001\) D'après le diagramme de Moody \(f=0.021\)
Indice
Calcule de \(K_c\) :
\(K_c = 0.14\)
Solution
Finalement \(\Delta H = 2.2\ m\)