TD 1 exercice 2
Exercice 2
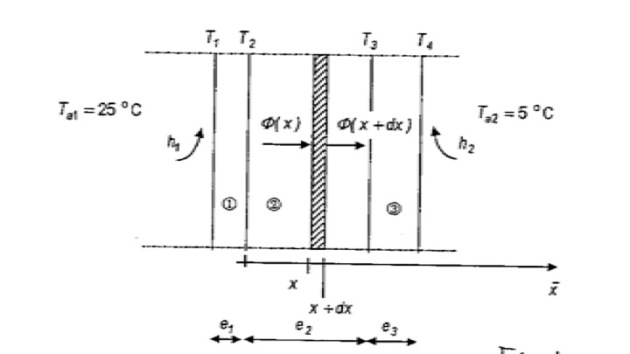
La paroi de la figure est composée de trois milieux :
le milieu 1 d'épaisseur e1 = 0,03 m et de conductivité thermique \(k_1 = 0,04 W\ m^{-1}\ K^{-1}\).
le milieu 2 d'épaisseur e2 = 0,40 m et de conductivité thermique \(k_2 = 1.50 W\ m^{-1}\ K^{-1}\).
le milieu 3 d'épaisseur e3 = 0,05 m et de conductivité thermique \(k_3 = 10 W\ m^{-1}\ K^{-1}\).
Une réaction exothermique dégage une puissance volumique \(\dot q = 103 W\ m^{-3}\) dans le milieu 2. On note \(h_1 = 100 W\ m^{-2}\ K^{-1}\) le coefficient d'échange par convection entre la paroi 1 et le milieu extérieur à la température \(T_{a1} = 25\ °C\) et \(h_2 = 150 W\ m^{-2}\ K^{-1}\) le coefficient d'échange par convection entre la paroi 2 et le milieu extérieur à la température \(T_{a2} = 5\ °C\).
Question
On étudie le régime permanent.
1. A partir d'un bilan thermique au sein du milieu 2, retrouver l'équation différentielle à laquelle doit satisfaire la température de ce milieu. Déterminer ensuite l'expression de la température \(T(x)\) du milieu 2 en fonction de \(\dot q\), \(k_2\), \(e_2\), \(T_2\) et \(T_3\).
Indice
Equation de la chaleur :
\(\Delta T-\frac 1 \alpha \frac{\partial T}{\partial t}+ \frac{\dot q}{k} = 0\)
et donc, ici :
\(\Delta T+ \frac{\dot q}{k_2} = 0\)
Indice
Il suffit alors d'intégrer deux fois l'équation suivante :
\(\frac{d^2 T(x)}{d x^2}=-\frac{\dot q}{k_2}\)
soit :
\(\frac{d T(x)}{d x}=-\frac{\dot q}{k_2}x+A\)
et
\(T(x)=-\frac{\dot q}{2k_2}x^2+Ax+B\)
Indice
CL :
\((1) T(x=0)=T_2\)
\((2) T(x=e_2)=T_3\)
La condition aux limite(1) permet de déterminer l’expression de la constante \(B\) :
\(B=T_2\)
La condition aux limite(2) permet de déterminer l’expression de la constante \(A\) :
\(A=\frac{T_3-T_2}{e_2}+\frac{\dot qe_2}{2k_2}\)
Solution
Il suffit de remplacer ces constantes d'intégration par leur expressions pour obtenir l'expression de la température \(T(x)\) dans le milieu 2 :
\(\frac{T(x)-T_2}{T_3-T_2}=-\frac{\dot q}{2k_2\left(T_3-T_2 \right)}x^2+\left[ \frac{1}{e_2}+\frac{\dot q e_2}{2 k_2\left( T_3-T_2\right)}\right]x\)
Question
2. Déterminer l'expression de la densité de flux \(\varphi(x)\) du milieu 2 en fonction de \(\dot q\), \(k_2\), \(e_2\), \(T_2\) et \(T_3\).
Indice
La densité de flux à pour expression :
\(\varphi (x)=-k_2\frac{dT(x)}{dx}\)
Solution
On déduit l'expression de la densité de flux de l'expression de la température \(T(x)\).
\(\varphi(x)=\dot qx-[T_3-T_2]\frac{k_2}{e_2}-\dot q\frac{e_2}{2}\)
Question
3. Calculer les températures \(T_1, T_2, T_3\) et \(T_4\). On commencera par déterminer \(T_2, T_3.\)
Indice
On commence par déterminer \(T_2\) et \(T_3\) en exprimant la continuité de la densité de flux à l'abscisse \(x=0\) et à l'abscisse \(x=e_2\).
Première équation : continuité de flux à en \(x=0\)
\(\frac{T_{a1}-T_2}{\frac{1}{h_1}+\frac{e_1}{k_1} }=\varphi(x=0)=-\left[T_3-T_2\right] \frac{k_2}{e_2}-\dot q\frac{e_2}{2}\)
Indice
On obtient finalement :
\(5.066T_2-3.75T_3=232.89\)
Indice
Seconde équation : continuité de flux à en \(x=e_2\)
\(\frac{T_{3}-T_{a2}}{\frac{1}{h_2}+\frac{e_3}{k_3} }=\varphi(x=e_2)=-\left[T_3-T_2\right] \frac{k_2}{e_2}+\dot q\frac{e_2}{2}\)
Indice
On obtient finalement :
\(3.75T_2-89.46T_3=-628.57\)
Indice
2 équations 2 inconnues
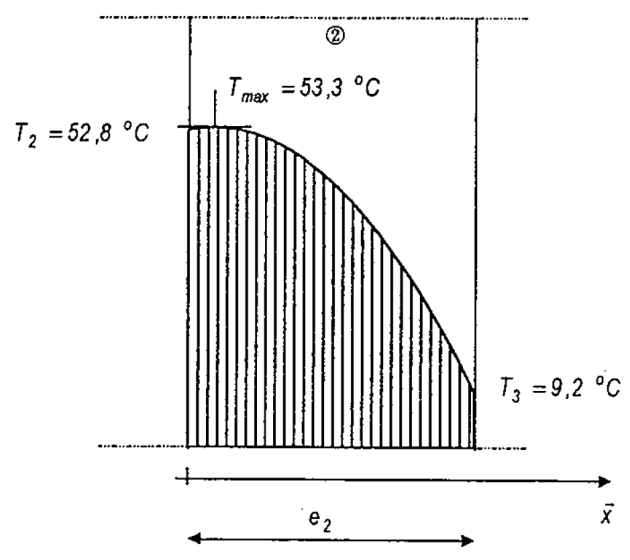
\(T_2 = 52.8\ °C\) et \(T_3 = 9.2\ °C\)
Il reste à calculer \(T_1\) et \(T_4\)
Indice
On exprime une nouvelle dois la continuité de la densité de flux.
Expression de la température \(T_1\) :
\(h_1\left(T_{a1}-T_1 \right)=\left(T_1-T_2 \right)\frac{k_1}{e_1}\)
Indice
Expression de la température \(T_4\) :
\(h_2\left(T_{4}-T_{a2} \right)=\left(T_3-T_4 \right)\frac{k_3}{e_3}\)
Solution
\(T_1=25.4\ °C\) et \(T_4=7.4\ °C\)
Question
4. Calculer la température maximale \(T_{max}\) au sein du milieu 2 ainsi que l'abscisse \(x_{max}\) correspondante.
Indice
La température maximale est atteinte lorsque la dérivée de la fonction T(x) s'annule ; on en déduit l'expression suivante :
\(\frac{dT}{dx}=0=-\frac{\dot q}{k_2}x_{max}+\frac{T_3-T_2}{e_2}+\frac{\dot q e_2}{2k_2}\)
Indice
\(x_{max}=\frac{(T_3-T_2)k_2}{\dot qe_2}+\frac 1 2 e_2=0.037\)
Indice
la dérivée seconde de la fonction est négative, il s'agit donc bien d'un maximum. L'expression de la température \(T(x)\) permet de calculer la valeur \(T_{max}\)
\(T(x) = -333.33x^2+24.41x+52.81\)
Solution
\(T_{max}=53.3\ °C\)
Question
5. Tracer la courbe représentative de la température du milieu 2.